

To show that two triangles are congruent, it is not necessary to show that all six pairs of corresponding parts are equal. These parts are equal because corresponding parts of congruent triangles are congruent. In Figure, Δ BAT ≅ Δ ICE.Įxample 1: If Δ PQR ≅ Δ STU which parts must have equal measurements? Congruent triangles are named by listing their vertices in corresponding orders.
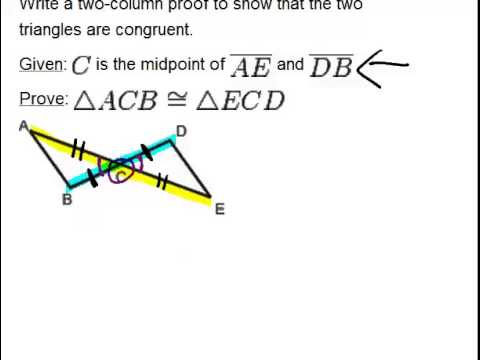
This means that Corresponding Parts of Congruent Triangles are Congruent (CPCTC). The parts of the two triangles that have the same measurements (congruent) are referred to as corresponding parts. The triangles in Figure 1 are congruent triangles. Two triangles are congruent when the three sides and the three angles of one triangle have the same measurements as three sides and three angles of another triangle. Triangles that have exactly the same size and shape are called congruent triangles. Summary of Coordinate Geometry Formulas.Slopes: Parallel and Perpendicular Lines.Similar Triangles: Perimeters and Areas.Proportional Parts of Similar Triangles.Formulas: Perimeter, Circumference, Area.Proving that Figures Are Parallelograms.Triangle Inequalities: Sides and Angles.Special Features of Isosceles Triangles.Classifying Triangles by Sides or Angles.Lines: Intersecting, Perpendicular, Parallel.Btw, this book is the No.1 statistical book I found ever for SAS programmers without statistical background. ReferenceĪppendix F – Data Transformations in Common Statistical Methods for Clinical Research with SAS Examples by Glenn Walker and Jack Shostak supplies a concise discussion on log-transformation. The SQL solution I used above, exp(mean(log(TestAUC))), is much simpler, and most important, it reminds us the applying of log-transformation. If 0 then set auc(keep=TestAUC) nobs=nobs īoth methods return to the geometric mean of TestAUC as 78.314997096.
Proc transpose data=auc (keep=TestAUC) out=test prefix=t So, if need the geometric mean of a variable, TestAUC for example, you should transpose the rows to columns or similarly, use a array: It takes a list of values as argument, which means, it can only perform on rows, but not on columns. In SAS/Base, GEOMEAN function is used to calculate the geometric mean. For details of equivalence testing, I may extend it into a separated note. So, in the analysis, the original values are transformed to geometric mean ratio (0.9412 with 90% limit of ) to compare with the predefined bounds. Suppose two treatment groups available, 1 and 2.įew extremely important conclusions, just as the codes above suggested, exp=exp is just geometric mean of X, and the geometric mean ratio, geomean (X1) / geomean(X2), simply equals exp-This is the mathematical equivalence of ratio and difference.īack to the AUC example, the FDA endorsed equivalence bounds offered, 0.8 and 1.25, which are both ratio values. Usually, AUC data mentioned above (Area Under Curve, which is based on blood levels) and antibody titer values are log-normal distributed(source data, noted as X), which means, if you take a log-transformation against X, namely Y=log(X), then Y follows the normal distribution (then Y has good properties to perform further statistical analysis). Both GMT and GMTR are wildly presented in statistical analysis reports. In vaccine trials (I worked before) where the interested values are antibody titers, the geometric mean is also called Geometric Mean Titer (GMT), while geometric mean ratio referred as Geometric Mean Titer Ratio (GMTR, also named “n-fold rise”). You can prove it mathematically by playing some log-transformations: 315⁄ 83.2077 (the ratio of two geometric means) simply gets 0.941199 (geometric mean ratio), which can be also derived by calculating the geometric mean of a ratio (see above). Similarly,ĬALCULATED gmTest / CALCULATED gmRef as gmrħ8. It can also be calculated manually byĪctually this kind of geometric mean (of a ratio) is more often called geometric mean ratio(a ratio of two geometric means, in this case, geometric mean of TestAUC and geometric mean of RefAUC). In a example, TTEST procedure reports a geometric mean as 0.9412, which is the geometric mean of a ratio, TestAUC/RefAUC. Just read since SAS 9.2, the TTEST procedure also natively supports Equivalence Test by simply adding a TOST option (Two one-sided tests). _ Programmers Need to Learn Statistics Or I will Kill Them All –Zed A.


 0 kommentar(er)
0 kommentar(er)
